Libuv 源码分析(6):数据结构—复合类型(队列)

一、概述

Libuv 用到了一些复合类型的数据结构：队列( Queue )、最小二叉堆( Binary min heap )、红黑树( R-B tree )等。其中队列和最小二叉堆是以宏的形式实现的。
本文主要分析 Libuv 队列。

二、Libuv 队列

各种队列、环形队列的各种实现大致相同又各有差异，本文主要关注 Libuv 对队列的实现。
Libuv 中的队列是以双向链表实现的环形(循环)队列。队列的节点的数据类型是”包含两个指针元素的指针数组”，节点的两个元素的值都是指针，指向另(或同)一个节点。节点的 0 号元素指向队列中的下一个节点，1 号元素指向队列中的上一个的节点。

约定: 环形队列的节点是”包含两个指针元素的指针数组”，而”包含两个指针元素的指针数组”不一定是节点。节点的两个元素都指向其他节点或本节点。如果节点在队列中，节点被其他节点或本节点的元素指向两次。当然，在进行入列、出列等操作过程中，会暂时打破这里对节点的约定，但最终能够得到恢复。

图1: 包含多个节点的队列。

图2：只有一个节点的队列(空队列)。特别地，前者可称之为空节点。后者不是环形队列，本文接下来的内容不会用到。

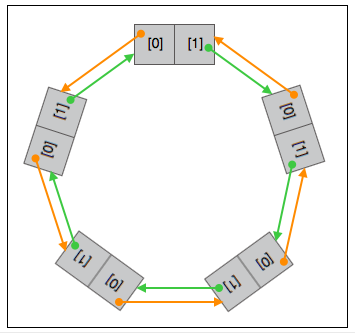
Libuv 中如果队列仅包含一个节点，并且该节点的 0 号元素，即节点的下一个节点指向本节点，则该队列为空，称该队列为空队列。是空队列还是空节点要看在怎样的上下文中。

单纯的队列几无用处。但是当其中一个节点是另一个结构的字段时，如 uv_loop_t 的 wq 字段，可通过字段在结构中的偏移量获取到结构的指针。详见 QUEUE_DATA 宏。

三、Libuv 队列分析准备

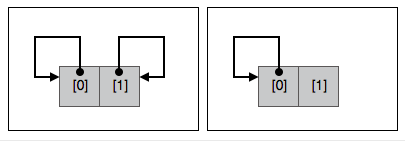
1、 x 变量

为方便分析，先定义”包含两个指针元素的指针数组”变量: void *x[2] ，类似于 uv_loop_s 的 wq 字段。请注意这里没说 x 一定是队列的的节点。下文会经常用到的 x 变量。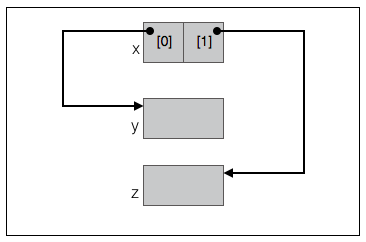

图3：变量 x 及其储值，这里不关心 y 和 z 是什么结构以及 y 和 z 是否是同一个对象。

2、数组指针、节点指针和队列指针

先想象一个普通的数组 int a[2] ，&a 的值虽然和 &a[0] 的值相同，但它们的意义却不同，&a 是指向数组的指针，&a[0]是指向数组 0 号元素的指针(数组名 a 在此不说)。
假设有三个变量 q、h、n ，它们都是 void *x[2] 指针数组的指针，赋予它们三种意义：
① 指向”包含两个指针元素的指针数组”的指针。包括：QUEUE_INIT 的宏参数 q ，以及 QUEUE_INIT 宏实现过程用到的的 QUEUE_NEXT 和 QUEUE_PREV 的宏参数 q 。
② 指向节点的指针。
③ 指向队列的指针。和 ② 经常进行角色转换。

图4: q 与指针数组、队列节点和队列的关系。

在不同的上下文，q 可以认为是指向”包含两个指针元素的指针数组”的指针或指向节点 x 的指针；也可以认为是指向的队列的指针。

约定： 如果认为 q 是指向队列的指针，这时简称队列为 “队列 q “，节点 x 称为 “队列 q 的根节点”，节点 x 的 0 号元素指向的节点 y 称为 “队列 q 的头节点”，节点 x 的 1 号元素指向的节点 z 称为 “队列 q 的尾节点”。

四、Libuv 队列实现分析

Libuv 队列是以宏实现的。宏分为私有和公开。所谓私有宏，用户代码也可以使用。包括 Libuv 也没严格遵守所谓的私有。

注：在宏中对队列的任何操作，如入列、出列也包括初始化等，产生的最终结果都要保持目标队列作为环形队列的特征。

1、辅助

typedef void *QUEUE[2];

/* Private macros. */
#define QUEUE_NEXT(q)       (*(QUEUE **) &((*(q))[0]))
#define QUEUE_PREV(q)       (*(QUEUE **) &((*(q))[1]))
#define QUEUE_PREV_NEXT(q)  (QUEUE_NEXT(QUEUE_PREV(q)))
#define QUEUE_NEXT_PREV(q)  (QUEUE_PREV(QUEUE_NEXT(q)))

1.1 QUEUE 类型

QUEUE 是一个”包含两个指针元素的指针数组”的类型的别名。

1.2 QUEUE_NEXT(q)

说明：
首先要明确，这里的宏参数 q 至少是指向的”包含两个指针元素的指针数组”的指针。 q 也可以是指向节点的指针，还可以是指向队列的指针(除非知道自己在做什么)。

作用：
取 q 指向的数组的 0 号元素——一个指向、或将要指向另(或同)一个节点的指针。

算法:
无

分析:
为方便分析，参考 QUEUE_INIT 中的语句:

QUEUE_NEXT(q) = (q);

通常 q 就算不是节点指针，也是指向”包含两个指针元素的指针数组”的指针，将上面定义的 x 变量取地址代入宏：

QUEUE_NEXT(&x) = (&x);

宏展开后(注：这里的两个 & 都是取地址符而非位与运算符):

(*(QUEUE **) &((*(&x))[0])) = (&x);

最外层的()是出于运算符优先级的考虑，在本例中不存在这个问题，去掉:

*(QUEUE **) &((*(&x))[0]) = &x;

x 先取地址再解指针引用，也是出于运算符优先级的考虑，在本例中不存在这个问题，等同于(本例中，实际上 &x 的值等于 x ，也等于 &x[0] )：

*(QUEUE **) &(x[0]) = &x;

暂时省去 (QUEUE **):

* &(x[0]) = &x;

先取地址再解指针引用，省去:

x[0] = &x;

竟然是直接给数组的 0 元素赋值。

为什么不像如下两种方式定义 QUEUE_NEXT ，而要搞这么复杂呢？

a. #define QUEUE_NEXT(q)          ((*(q))[0])

这样会丢失类型信息。如果这样定义，类似 QUEUE_PREV_PREV 这种嵌套使用将无法工作:

#define QUEUE_NEXT_PREV(q) (QUEUE_PREV(QUEUE_NEXT(q)))

QUEUE_NEXT(q) 的值如果是 void * 类型，外层的 QUEUE_PREV 宏无法工作。

b. #define QUEUE_NEXT(q)       ((QUEUE *) ((*(q))[0]))

这样是一个常量，不是左值，即无法赋值。如果这样定义，类似如下操作就会失败：

QUEUE_NEXT(q) = (q);

所以表达式 (*(QUEUE **) &((*(q))[0])) 既带有类型信息，又是一个左值——亦即可以通过 *r = value 赋值，也可以通过 *r 取值。

实际上有种更好理解但看起来没这么”酷”的定义这 4 个宏的方式：

#define QUEUE_NEXT(q)       ((*(q))[0])
#define QUEUE_PREV(q)       ((*(q))[1])
#define QUEUE_PREV_NEXT(q)  (QUEUE_NEXT((QUEUE *)QUEUE_PREV(q)))
#define QUEUE_NEXT_PREV(q)  (QUEUE_PREV((QUEUE *)QUEUE_NEXT(q)))

上述实现将类型强制转换的操作转移到 QUEUE_NEXT_PREV 和 QUEUE_PREV_NEXT 中。
但让 QUEUE_NEXT 和 QUEUE_PREV 看起不知道结果是什么类型但并不影响使用，下面的语句可以进行隐式类型转换:

void *x[2] = ...;
QUEUE *node = QUEUE_NEXT(&x); // QUEUE *node = (*(&x))[0]; QUEUE *node = x[0];

1.2 QUEUE_PREV(q)

类似于 QUEUE_NEXT ，作用是：取 q 指向的节点的 1 号元素——一个指向、或将要指向另(或同)一个节点的指针。

1.3 QUEUE_PREV_NEXT(q)

#define QUEUE_PREV_NEXT(q)  (QUEUE_NEXT(QUEUE_PREV(q)))

作用是：取 q 指向的节点的 1 号元素，是一个指向另(或同)一个节点的指针，再取指针指向的数组的第 0 个元素——还是一个指向另(或同)一个节点的指针。

1.4 QUEUE_NEXT_PREV(q)

#define QUEUE_NEXT_PREV(q)  (QUEUE_PREV(QUEUE_NEXT(q)))

类似于 QUEUE_PREV_NEXT ，作用是：取 q 指向的节点的 0 号元素，是一个指向另(或同)一个节点的指针，再取指针指向的数组的 1 号元素——还是一个指向另(或同)一个节点。

总之，上述 4 个宏，都作用在一个”包含两个指针元素的指针数组”的其中一个元素上，类似于操作 x[0] 或 x[1] 。作为右值时，结果都是:返回一个指向节点的指针，也有可能是本数组(本节点，如果指针数组是节点的话)的指针；作为左值时，作用都是: 为数组元素赋值为指向节点的指针，也有可能是本数组(本节点，如果指针数组是节点的话)的指针。

2、初始化

#define QUEUE_INIT(q)                                                         \
  do {                                                                        \
    QUEUE_NEXT(q) = (q);                                                      \
    QUEUE_PREV(q) = (q);                                                      \
  }                                                                           \
  while (0)

说明：
首先要明确， q 至少是指向的”包含两个指针元素的指针数组”的指针。
q 也可以是指向节点的指针或者指向队列的指针，但一般不会。如果队列刚刚被初始化仅包含 1 个节点，重复初始化没必要；如果队列有 2 个或 2 个以上的节点，再次初始化就打破了队列的环形。

作用：
初始化节点。输入一个指向”包含两个指针元素的指针数组”的指针，将数组初始化为一个节点，节点未在任何队列中。而该指针提升成为了指向一个节点的指针。
另外还可以这样认为：初始化队列。输入一个指向”包含两个指针元素的指针数组”的指针，将数组初始化为空队列的节点。而该指针提升成为了指向一个空队列的指针。
这两种说法很让人纠结。下面的分析按第一种说法来。

算法：
① 将数组的头指针指向本节点。
② 将数组的尾指针指向本节点。
③ 最终使数组成为一个节点。q 从一个单纯的指向”包含两个指针元素的指针数组”的指针，提升为指向节点的指针。

分析：
假设有定义, void *x[2] 。 &x 对应 q 。QUEUE_INIT 做的工作是：

x[0] = &x;
x[1] = &x;

让 q 指向的”包含两个指针元素的指针数组”的两个元素的值都等于 q，也就是两个元素保存的值是数组本身的内存地址。

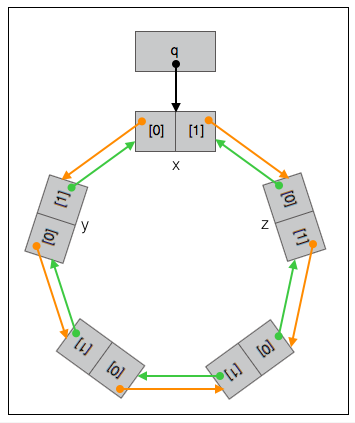
图示：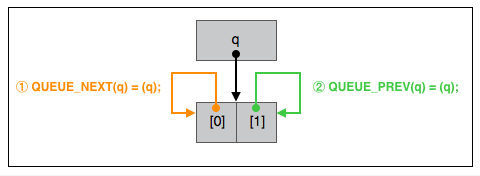

图5: `QUEUE_INIT(q)` 初始化 q

其他：
QUEUE_INIT 的宏参数，以及宏实现使用的 QUEUE_NEXT 和 QUEUE_PREV 的宏参数，是唯一一处可以将 q 单纯认为是”包含两个指针元素的指针数组”的地方。其他地方 q 、h 、 n 看作要么是指向节点的指针，要么是指向队列的指针——又陷入某种纠结。

3、在队列尾插入节点

#define QUEUE_INSERT_TAIL(h, q)                                               \
  do {                                                                        \
    QUEUE_NEXT(q) = (h);                                                      \
    QUEUE_PREV(q) = QUEUE_PREV(h);                                            \
    QUEUE_PREV_NEXT(q) = (q);                                                 \
    QUEUE_PREV(h) = (q);                                                      \
  }                                                                           \
  while (0)

说明：
首先要明确，这里的宏参数 h 是指向队列的指针； q 可以是单纯的”包含两个指针元素的指针数组”的指针，也可以是指向节点的指针(或者说 q 指向一个空队列，但不能是包含 2 个或 2 个以上节点的队列)。如果要合并队列，即将源队列的所有节点添加到目标队列，请使用 QUEUE_ADD 。

作用：
入列。简单说法：在队列 h 尾部插入节点 q 。严格说法：在 h 指向的队列尾部插入 q 指向的节点。

算法：
① 节点 q 的上一节点设置为队列 h 的根节点。(作用在 节点 q 上)
② 节点 q 的下一节点设置为队列 h 的尾节点。(作用在 节点 q 上)。通过 ① 和 ② ，节点 q 依附到了队列 h 的尾部。
③ 队列 h 的原尾节点的下一节点设置为节点 q 。(作用在 h 指向的原尾节点上)
③ 队列 h 的根节点的下一节点设置为节前 q 。(作用在 h 指向的根节点上)
最终节点 q 成为队列 h 新的尾节点。

分析：
假设有定义, void *x[2] , void *y[2] 。&x 对应 h , &y 对应 q 。 QUEUE_INSERT_TAIL 做的工作是：

y[0] = &x;
y[1] = &(x[1]);
x[1][0] = &y;
x[1] = &y;

x[1][0] = &y; 这行直接运行不过的，而 (*(QUEUE *)x[1])[0] = &y; 虽可以但注意力就转到它处了，保持这行错误的反而容易理解。至于为什么运行不过，原因见上。

图示：
考虑 3 种情况：
① 队列 h 包含 1 个节点(空队列)，队列的头节点、尾节点和根节点是同一个节点。
② 队列 h 包含 2 个节点，队列的头节点和尾节点是同一个节点。
③ 队列 h 包含 3 个或三个以上节点，队列的头节点和尾节点是不同的节点。
因为在队列尾部插入节点，除了第一种情况，并不涉及到头节点，从这个角度来看实际上就两种情况。

图6: 队列 h 包含 1 个节点(空队列)  图7: 队列 h 包含 2 个节点  图8: 队列 h 包含 3 个或三个以上节点

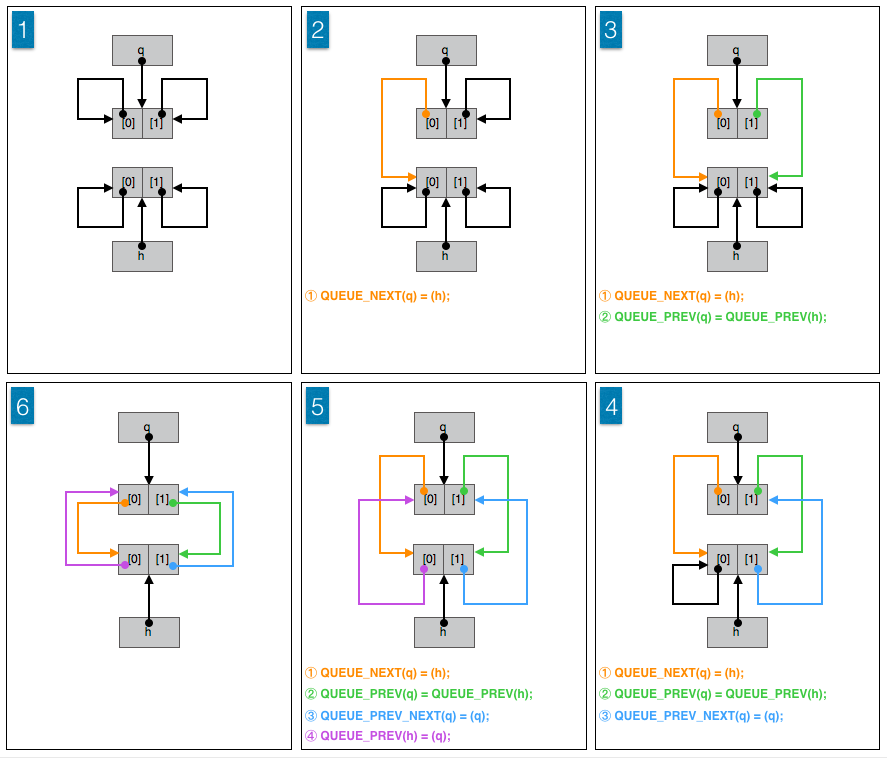
其他：
事实上， QUEUE_PREV_NEXT(q) = (q); 可以改为 QUEUE_NEXT(h) = (q); 。

4、在队列头插入节点

#define QUEUE_INSERT_HEAD(h, q)                                               \
  do {                                                                        \
    QUEUE_NEXT(q) = QUEUE_NEXT(h);                                            \
    QUEUE_PREV(q) = (h);                                                      \
    QUEUE_NEXT_PREV(q) = (q);                                                 \
    QUEUE_NEXT(h) = (q);                                                      \
  }                                                                           \
  while (0)

插队，在队列 q 头部插入 h 节点。本人最讨厌谁插队，而且是直接插到头。该操作类似于 QUEUE_INSERT_HEAD ，不再分析。
另，事实上， QUEUE_NEXT_PREV(q) = (q); 可以改为 QUEUE_PREV(h) = (q); 。

5、获取头节点

#define QUEUE_HEAD(q)                                                         \
  (QUEUE_NEXT(q))

说明：
注意并非出列操作。

作用：
简单说法：获取队列 q 的头节点。严格说法：获取 q 指向的队列的头节点。

算法：
无

分析：
无

图示：
无

其他：
无

6、删除节点

#define QUEUE_REMOVE(q)                                                       \
  do {                                                                        \
    QUEUE_PREV_NEXT(q) = QUEUE_NEXT(q);                                       \
    QUEUE_NEXT_PREV(q) = QUEUE_PREV(q);                                       \
  }                                                                           \
  while (0)

说明：
q 必须是在队列中的非根节点。先使用 QUEUE_HEAD 获取到队列的头节点，再使用 QUEUE_REMOVE 可达到出列的作用。 如果对队列的根节点进行删除操作，将会对队列造成破坏。

作用：
将节点 q 从所在的队列中删除。

算法：
① 节点 q 的上一节点的下一个节点原本是节点 q 自己，让其设置为节点 q 的下一个节点。(作用在节点 q 的上一个节点上)
② 节点 q 的下一节点的上一个节点原本是节点 q 自己，让其设置为节点 q 的上一个节点。(作用在节点 q 的下一个节点上)。通过 ① 和② ，节点 q 依附到了队列 h 的尾部。

分析：
无

图示：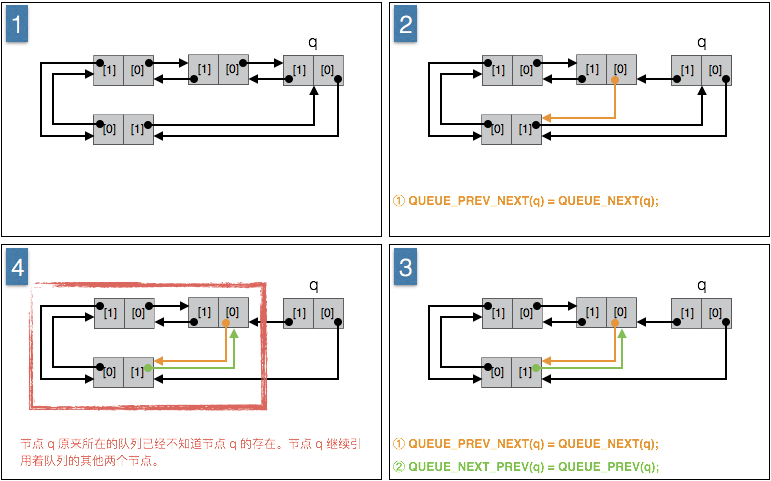

图9: 删除节点

其他：
对空队列的唯一的根节点进行删除操作不会有任何效果。

7、遍历元素

/* Important note: mutating the list while QUEUE_FOREACH is
 * iterating over its elements results in undefined behavior.
 */
#define QUEUE_FOREACH(q, h)                                                   \
  for ((q) = QUEUE_NEXT(h); (q) != (h); (q) = QUEUE_NEXT(q))

说明：
使用时需小心，宏中的 for 循环并不完整。 h 是一个队列， q 的类型是 QUEUE * 。

作用：
遍历队列，将从头节点到尾节点循环赋值给变量 h 。其中包括头节点和尾节点。

算法：
无

分析：
无

图示：
无

其他：
无

8、判断队列是否为空

#define QUEUE_EMPTY(q)                                                        \
  ((const QUEUE *) (q) == (const QUEUE *) QUEUE_NEXT(q))

如果队列 q 的头节点是自身，则认为队列 q 是空队列。注意，`QUEUE_EMPTY` 如果认为一个队列是空队列，但该队列不一定是环形队列。

9、合并队列
#define QUEUE_ADD(h, n)                                                       \
  do {                                                                        \
    QUEUE_PREV_NEXT(h) = QUEUE_NEXT(n);                                       \
    QUEUE_NEXT_PREV(n) = QUEUE_PREV(h);                                       \
    QUEUE_PREV(h) = QUEUE_PREV(n);                                            \
    QUEUE_PREV_NEXT(h) = (h);                                                 \
  }                                                                           \
  while (0)

说明：
并非入列操作。根据上下文和语义， h 和 n 必须是队列，都可以为空队列。而如果 n 为节点，则会破坏其原来所在的队列。

作用：
将队列 n 的节点按顺序合并入队列 h 的尾部。

算法：
① 队列 h 的尾节点的下一个节点原本是队列 h 的根节点，将其设置为队列 n 头节点。(作用在队列 h 的尾节点上)
② 队列 n 的头节点的上一个节点原本是队列 n 的根节点，将其设置为队列 h 尾节点。(作用在队列 n 的头节点上)
③ 队列 h 的新的尾节点设置为队列 n 的尾节点。(作用在队列 h 的根节点上)
④ 队列 h 的尾节点的现在是队列 n 的尾节点，将其设置为队列 h 的根节点。(作用队列 h 新的尾节点上，或者说作用在队列 n 的尾节点上)

分析：
无

图示：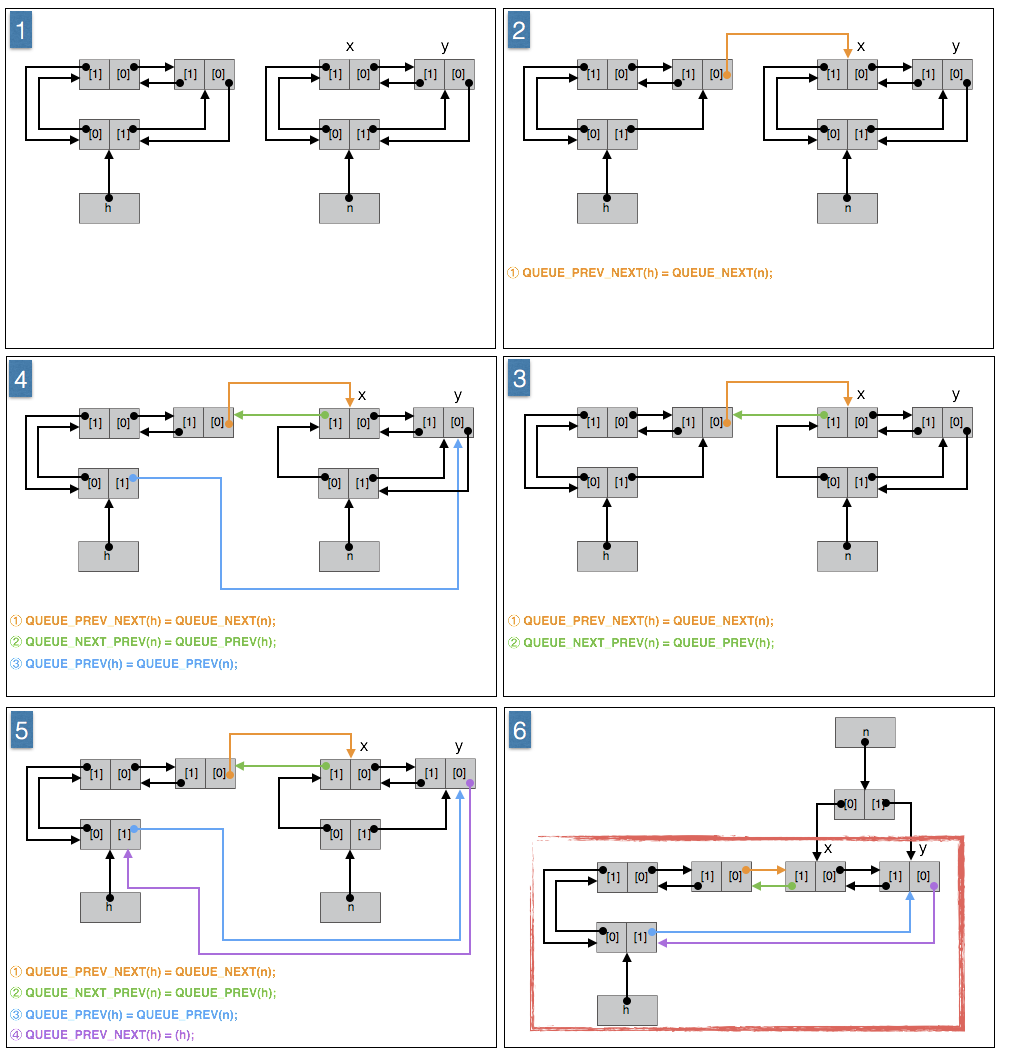

图10: 合并队列

其他：
无

10、分拆(分解)队列

#define QUEUE_SPLIT(h, q, n)                                                  \
  do {                                                                        \
    QUEUE_PREV(n) = QUEUE_PREV(h);                                            \
    QUEUE_PREV_NEXT(n) = (n);                                                 \
    QUEUE_NEXT(n) = (q);                                                      \
    QUEUE_PREV(h) = QUEUE_PREV(q);                                            \
    QUEUE_PREV_NEXT(h) = (h);                                                 \
    QUEUE_PREV(q) = (n);                                                      \
  }                                                                           \
  while (0)

说明：
h 是非空队列，q 必须是指向队列 h 其中一个非根节点的指针，n 是空队列。
如果 h 是空队列或 q 是指向队列 h 根节点的指针，则会破坏队列 h；如果 q 是其他队列的节点指针，则队列 h 以及其他队列都会遭到破坏；如果 n 是非空队列，则会破坏队列 n 。

作用：
将指针 q 指向的节点到队列 h 尾点之间的节点按顺序插入(移入)队列 n 的头部。包括指针 q 指向的节点和队列 h 的尾节点。

算法：
① 队列 n 的尾节点设置为队列 h 的尾节点。(作用在队列 n 的根节点上)
② 队列 n 的新的尾节点的上一个节点原本是队列 h 的根节点，将其设置为队列 n 的根节点。(作用在队列 n 的新的尾节点上，或者说作用在队列 h 的尾节点上)
③ 队列 n 的头设置为指针 q 指向的节点。(作用在队列 n 的根节点上)
④ 队列 h 的尾节点设置为指针 q 指向的节点的上一个节点。(作用在队列 h 的根节点上)
⑤ 队列 h 的尾节点的上一节点设置为队列 h 的根节点，也就是设置为指针 q 指向的节点的上一个节点。(作用在队列 h 的新的尾节点上，或者说作用在指针 q 指向的节点上)这时队列 h 恢复成合法的环形队列。
⑥ 指针 q 指向的节点的上一个节点设置为队列 q 的根节点。(作用在指针 q 指向的节点上，或者说作用在队列 n 的首节点上)

分析：
无
图示：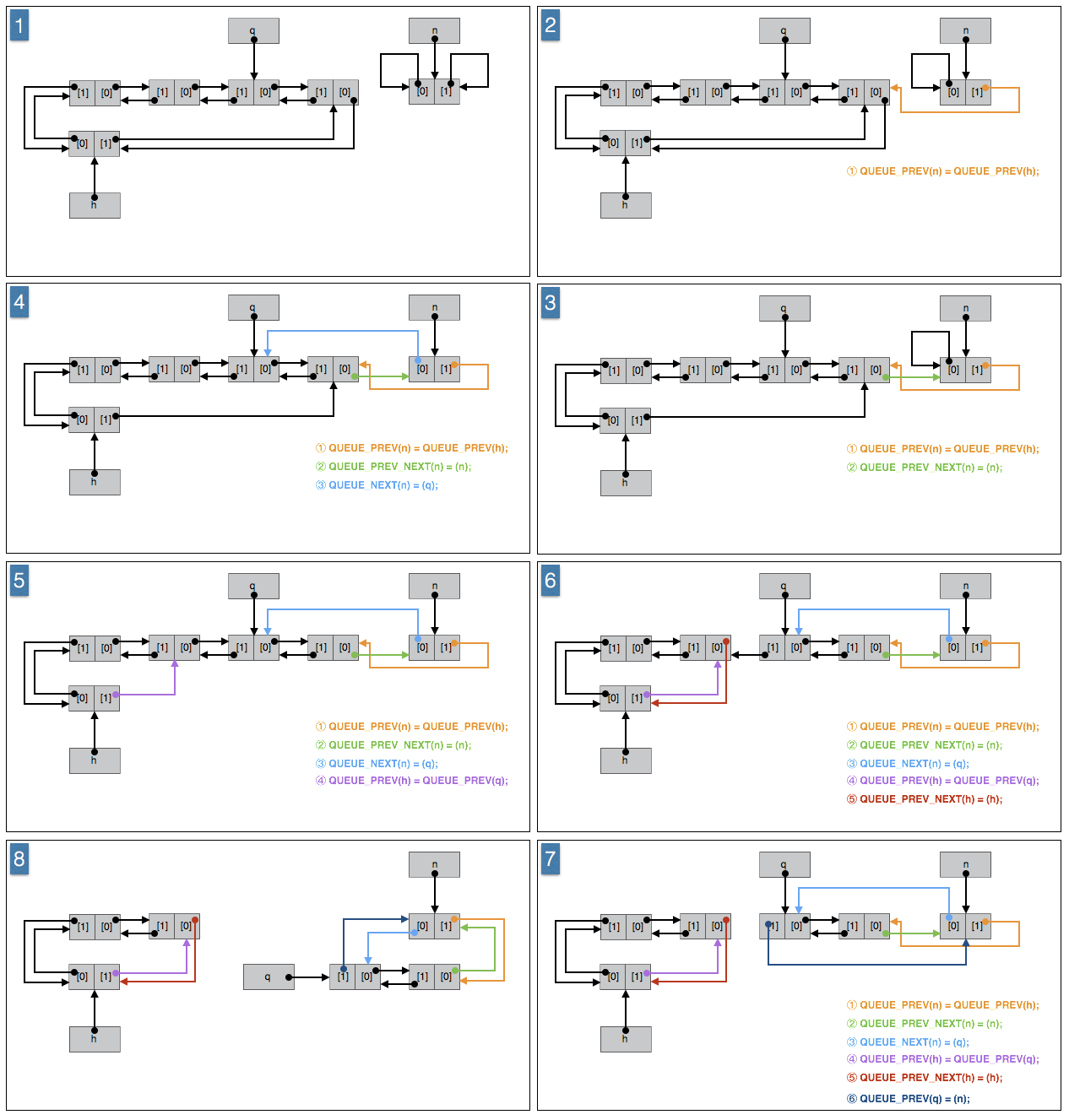

图11: 分拆(分解)队列

其他:
无

11、移动节点

#define QUEUE_MOVE(h, n)                                                      \
  do {                                                                        \
    if (QUEUE_EMPTY(h))                                                       \
      QUEUE_INIT(n);                                                          \
    else {                                                                    \
      QUEUE* q = QUEUE_HEAD(h);                                               \
      QUEUE_SPLIT(h, q, n);                                                   \
    }                                                                         \
  }                                                                           \
  while (0)

说明：
h 是可空队列，n 是空队列。如果 h 是空队列，则 n 会设置为空队列；如果 n 是非空队列，则会破坏队列 n 。

作用：
移动节点。将队列 h 从头节点到尾节点之间的节点按顺序插入(移入)队列 n 的头部。包括队列 h 的头节点和尾节点。

算法：
核心算法见 QUEUE_SPLIT 。

分析：
无

图示：
无

其他:
无

12、获取队列所在结构的指针

#define QUEUE_DATA(ptr, type, field)                                          \
  ((type *) ((char *) (ptr) - offsetof(type, field)))

QUEUE_DATA 是和队列操作无关的一个宏，但却是非常有用处的。 offsetof 宏用于求结构体中一个成员在该结构体中的偏移量。成员所在的内置地址往回移该偏移量，就是结构的内存地址。

参考资料

• macOS: queue(3) ( #import <Kernel/sys/queue.h> )
• FreeBSD: queue(3) ( #include <sys/queue.h> )
• https://en.wikipedia.org/wiki/Queue_(abstract_data_type)
• https://en.wikipedia.org/wiki/Value_%28computer_science%29#Assignment:_l-values_and_r-values
• http://www.jianshu.com/p/6373de1e117d